Bachelor's Thesis (Major Technical Project)
Executing robot skills by learning them from human video demonstrations

Overview
This research presents a novel approach for robotic task learning from human demonstrations using base vision transformer (ViT) models. The goal is to decompose complex tasks into fundamental sub-tasks that a robotic manipulator can execute with precision.
Key Contributions
- Vision Transformer-based task segmentation: Utilizes ViViT, Timesformer, and VideoMAE architectures to predict fundamental sub-tasks.
- Real-time Processing: masked autoencoding improves feature extraction to eliminate redundant information.
- Sub-task Decoding via Multi-Head MLP: Predicts action sequences for execution.
- Trajectory Learning with DMP: Dynamic Movement Primitives (DMP) generate smooth and adaptive robotic motions conditioned on varied environment.
Methodology
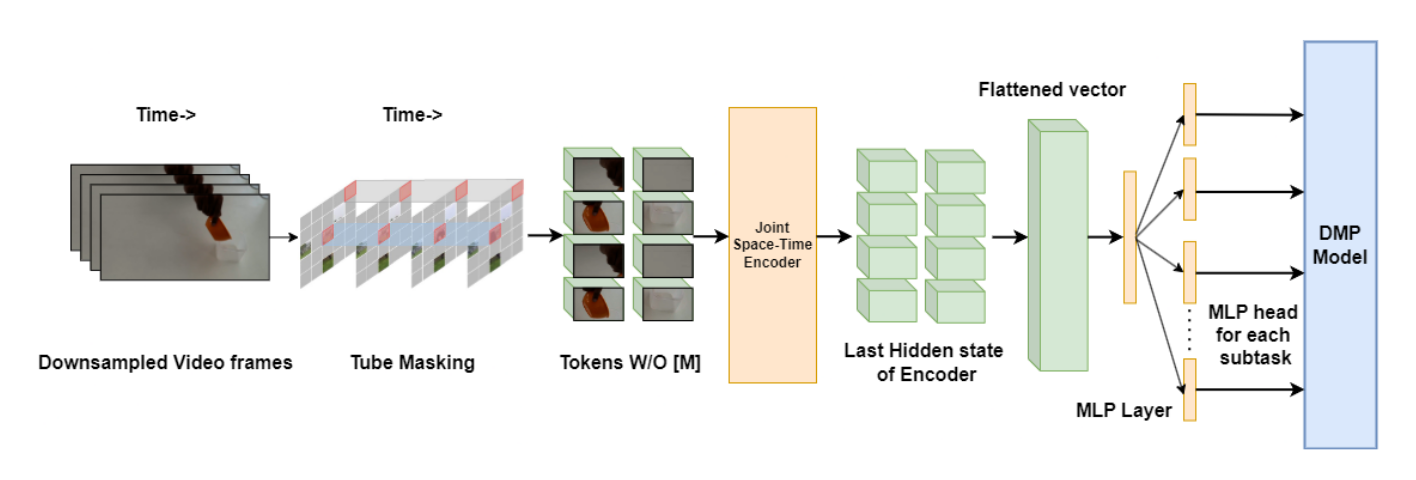
- Video Encoding: Human demonstrations are recorded and encoded using Vision Transformers.
- Sub-task Classification: Transformer embeddings are processed by a multi-head classifier to output task primitives.
- Trajectory Execution: Identified subtasks are executed using DMP-based motion planning. Each joint trajectory of the robotic manipulator is described using the following DMP equation: Equation:
τ ẍ = α(β(g − x) − τ ẋ) + f (x)where:-
τis the temporal scaling factor controlling movement duration. -
xis the position, ẋ is the velocity, and ẍ is the acceleration. -
gis the goal position the trajectory aims to reach. -
alphaandbetacontrols convergence speed—higher values lead to faster convergence, regulatethe spring-like behavior of the trajectory.. -
f(x)is the forcing function that ensures the trajectory follows a learned shape.
-
- Evaluation on Robotic Manipulator: The approach was tested on a 7-DOF Kinova Gen3 Robot.
Components of Movement primitives
1. Forcing Function
The forcing function shapes the trajectory based on learned data.
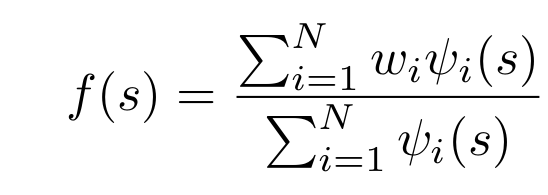
where:
- w_i represents the weight of each basis function.
- psi_i(s) is a basis function that provides flexibility in trajectory shaping.
2. Basis Function
DMP uses Gaussian basis functions to model smooth movements. The Gaussian basis function is given by:
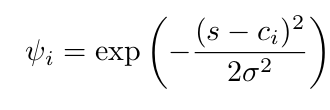
where:
- c_i is the center of the basis function.
- sigma determines the spread (width) of the Gaussian distribution.
3. Weight Estimation
The impact of each basis function on the trajectory is determined by its weight, which is computed using locally weighted regression:
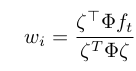
where:
- zeta depends on the phase variable, initial position y_0, and goal position g.
- Phi is a diagonal matrix, where each diagonal element corresponds to the value of the basis function psi at a specific time step.
4. Target Forcing Function
The target forcing function f_t is computed as:
f_t = (τ^2 * ẍ) - α * (β * (g - x) - τ * ẋ)
This equation ensures the robot learns and adapts its movements based on observed demonstrations.
Real-world experiments
| Model | Pick & Place | Pick & Pour | Mix | Moping | Overall Accuracy |
|---|---|---|---|---|---|
| ViViT | 76.00% | 68.00% | 46.00% | 70.83% | 65.00% |
| Timesformer | 88.00% | 76.00% | 58.00% | 54.16% | 71.20% |
| VideoMAE | 92.00% | 66.00% | 84.00% | 83.33% | 81.03% |
Findings:
- VideoMAE outperforms ViViT and Timesformer in recognizing sub-tasks accurately.
- Pick and Place tasks were successfully identified, while Pick and Pour showed some confusion.
- Mix and Moping tasks required refinement due to similar action primitives.